Í beinni
Kosningavaktin:
Nýjustu tíðindi

Fótbolti - La Liga
Real Sociedad - Barcelona
Innlent
Erlent
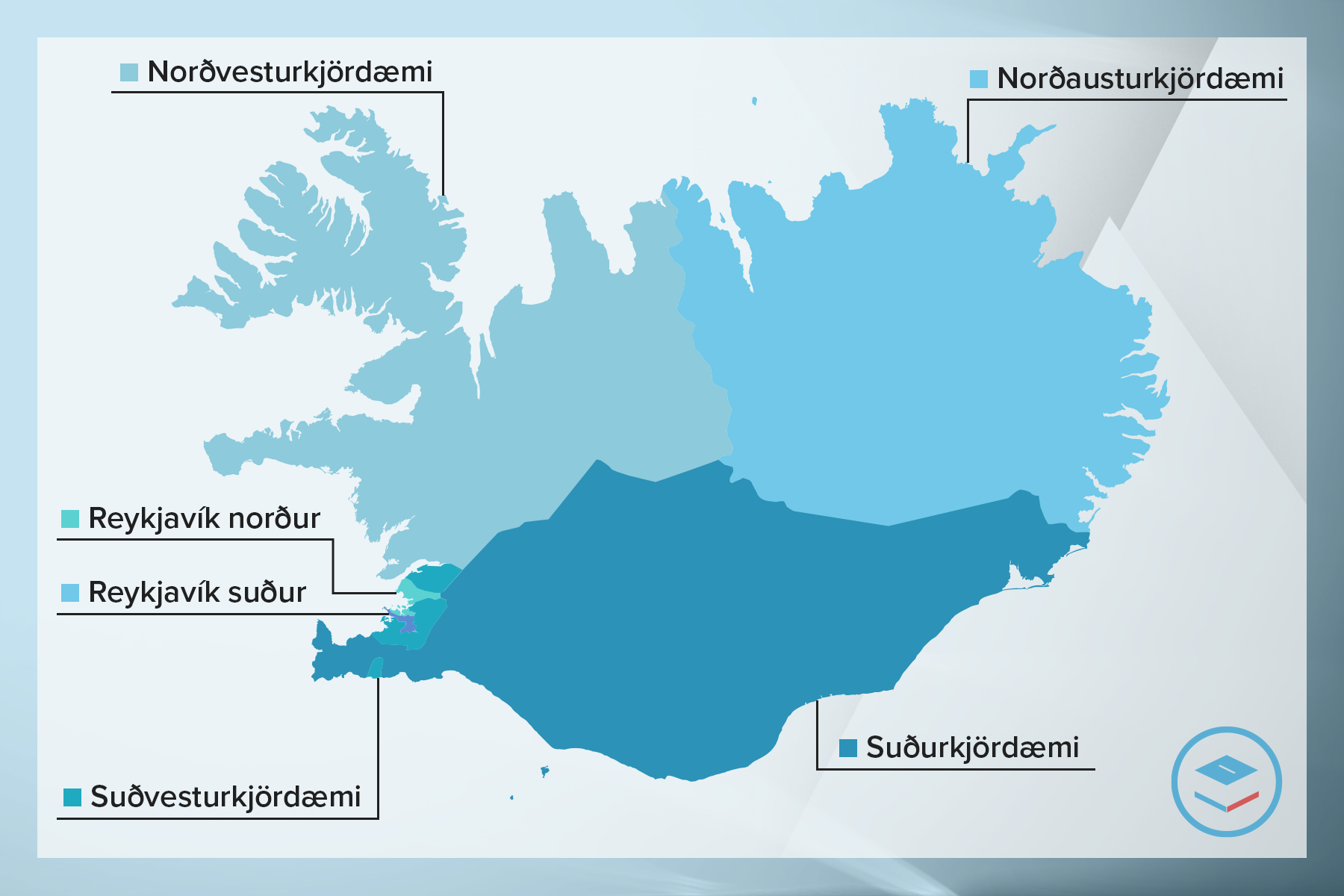
Kosningar 2024
Veður
Hádegisfréttir
Kvöldfréttir
Stjórnmál
Harris gegn Trump
Dómsmál
Andlát
Samtalið
Pallborðið
Kompás
Innlent
Erlent
Atvinnulíf
Neytendur
Kauphöllin
Seðlabankinn
Vistaskipti
Veitingastaðir
Samstarf
Fréttir af flugi
Fasteignamarkaður
Ferðaþjónusta
Staðan í deildum
Fótbolti
Körfubolti
Handbolti
Besta karla
Besta kvenna
Bónus karla
Bónus kvenna
Enski boltinn
Olís karla
Olís kvenna
NFL
Íslenski boltinn
Meistaradeildin
Golf
Rafíþróttir





